L’eleganza dell’anisocronismo del pendolo

La teoria dell’isocronismo del pendolo fu introdotta per la prima volta da Galileo Galilei nel 1592. Partiamo dall’etimologia del termine isocrono. Essa deriva dal greco isos  (uguale) e khronos (tempo). Isocronismo significa, quindi, uguale nel tempo e cioè a tempo costante. Inoltre c’è da precisare il fatto che il pendolo al quale si riferiva Galilei nella sua trattazione era quello semplice, detto anche matematico, consistente cioè in un sistema ideale costituito da una particella appesa ad un filo sottile inestensibile di massa trascurabile fissato ad un supporto. Tale pendolo, se spostato dalla sua posizione di equilibrio, oscilla in un piano verticale sotto l’azione del campo gravitazionale. Si trascurano inoltre tutti i possibili attriti. Galilei analizzò tale sistema per piccole oscillazioni, cioè per piccoli spostamenti dalla posizione di equilibrio. 

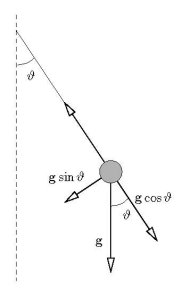
Proviamo ora ad analizzare le forze agenti sulla massa appesa al filo. Osservando la figura si vede che tali forze agenti sono il peso  della massa e la tensione  del filo. Visto che il moto del pendolo avviene su di un piano, scegliamo una coppia di assi ortogonali, uno diretto lungo la tangente al cerchio, l’altro lungo il suo raggio. La componente lungo il raggio del peso della massa  è bilanciata dalla tensione del filo . Per quanto concerne la componente tangenziale  (F è opposta alla direzione degli angoli  crescenti). Ora si utilizza l’ipotesi di piccoli angoli  per cui:

ottenendo quindi:

dove L è la lunghezza del filo e . Per piccoli spostamenti la forza di richiamo è quindi proporzionale ed opposta allo spostamento. Questa condizione è proprio quella del moto armonico semplice  con  e quindi si ottiene un periodo di oscillazione:

Così si dimostra utilizzando solo il secondo principio della dinamica l’isocronismo del pendolo per piccoli angoli, cosa che Galilei per primo misurò nella lucerna della cattedrale di Pisa vedendo il lampadario che oscillava dopo un intervento di spegnimento delle candele. Misurò il periodo utilizzando il battito del polso. Nella Cappella Aulla del Camposanto Monumentale si può oggi osservare la lampada votiva che era sospesa nella Cattedrale al tempo di Galileo. 

 

Lev Davidovic Landau

La dimostrazione dell’isocronismo del pendolo può essere effettuata secondo diversi procedimenti. A mio parere il più elegante e chiaro sta nel primo volume di Fisica teorica del grande scienziato Lev Davidovic Landau. Per seguire la sua dimostrazione dobbiamo prima definire le coordinate generalizzate come n grandezze qualsiasi () che caratterizzano completamente la posizione di un sistema con n gradi di libertà e una funzione detta lagrangiana che è un funzionale delle coordiante generalizzate, delle derivate rispetto al tempo delle coordinate generalizzate e del tempo stesso. Tale funzionale descrive completamente le equazioni del moto del sistema tramite il principio di Hamilton:

 

dove S definisce l’azione del sistema ed ha le dimensioni di un’energia per un tempo. Proprio grazie al principio di Hamilton si dimostra una splendida connessione fra la matematica e l’Universo nota come teorema di Noether che stabilisce che per ogni simmetria continua in un problema di fisica corrisponde una legge di conservazione. Tralasciando tali importantissime conseguenze occupiamoci ora, visto che abbiamo introdotto tutti gli stumenti matematici che ci serviranno, della dimostrazione fatta dal fisico russo. Per prima cosa definiamo come unidimensionale il moto del pendolo semplice perchè rappresenta un sistema con un solo grado di libertà. Questo diviene evidente se si pensa al fatto che è sufficiente l’angolo  per identificare completamente la posizione del pendolo. La forma più generale della funzione lagrangiana per un tale sistema, soggetto a condizioni esterne costanti (campo gravitazionale  costante), è

dove a(q) è una funzione della coordinata generalizzata q.In particolare se q è una coordinata cartesiana otteniamo:

Tale funzione lagrangiana si vede qui che è “legata” fisicamente al teorema di conservazione dell’energia meccanica per un sistema consevativo come il pendolo semplice. Avrete notato infatti che il secondo membro corrisponde all’energia cinetica del sistema meno l’energia potenziale gravitazionale. Il merito della dimostrazione di Landau sta proprio nel fatto che tramite tale trattazione non serve nemmeno scrivere l’equazione del moto del sistema; è comodo partire direttamente dal loro integrale primo, cioè dall’equazione che esprime la legge di conservazione dell’energia

Questa equazione differenziale del primo ordine si integra per semplice separazione di variabili:

da cui

con U(x)<E.

Considerando nel nostro caso il pendolo semplice utilizziamo come coordinata generalizzata l’angolo  per cui l’energia del sistema diventa:

dove  è l’angolo massimo di scostamento del filo dalla verticale. Essendo il periodo uguale al tempo quadruplicato impiegato per il percorso da 0 a , si ha:

Utilizzando ora le formule di bisezione , otteniamo:

Ponendo poi , tale integrale diventa:

Scritto in altro modo

dove

è un integrale ellittico di prima specie. Essa è la soluzione generale del problema del periodo di oscillazione di un pendolo che, come si vede, è anisocrono perchè dipendente dall’angolo  da cui viene inizialmente lasciato oscillare. Nel caso delle piccole oscillazioni  e quindi lo sviluppo della funzione K(k) ci dà:

Il primo termine di questo sviluppo corrisponde alla formula per il pendolo semplice per piccole oscillazioni trovata precedentemente. In questo caso si ricade quindi nell’isocronismo.

Nei secoli passati il pendolo è stato per l’uomo il migliore cronometro sfuttando il suo isocronismo per piccole oscillazioni. Visto che in realta tali piccole oscillazioni sono sempre difficilmente riproducibili per un orologio a pendolo, lo scarto nel periodo dato da oscillazioni più grandi era compensato da una scelta di un’ampiezza mantenuta costante. Il problema però che si presentava era la presenza di aria nell’orologio e non di vuoto. Ciò si ripercuoteva nell’attrito, una forza dissipativa che, produceva, nel migliore dei casi, una variazione di alcuni secondi sul tempo misurato. Ciò era evidentemente inacettabile per cui nel ‘600 Huygens escogitò un dispositivo per aggiungere energia al pendolo in modo da renderla costante. Tale sistema era costituito da una molla unita al pendolo tramite un dispositivo detto scappamento dell’orologio. Per comprendere quanto fosse importante la discussione in passato sull’isocronismo del pendolo, basti pensare che da esso dipendeva la corretta misurazione del tempo. Per ricordarcelo, le vecchie banconote da 2000 lire rappresentavano da un lato il ritratto di Galileo, dall’altro una lampada appesa nel Duomo di Pisa. Ciò che mi dispiace maggiormente per il passaggio ad una moneta unica europea è che non vedo più tale lampada abbastanza frequentemente.